Локальная система координат. Часть III

Незаметно пролетел еще один год и наш любимый Robot & Хобот отметил четырехлетие. Сегодня подошла очередь разобраться с узлами. Локальная система координат для узлов в Robot отсутствует и все операции по назначению нагрузок, опор и других атрибутов, необходимо проводить относительно глобальной системы координат. При создании узла, пользователь может использовать только декартову систему координат. 


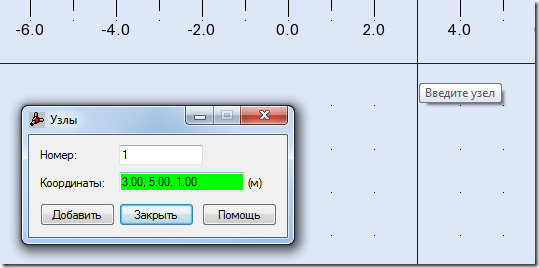
Однако узнать или изменить координаты существующего узла, мы можем также в полярной, цилиндрической и сферической системах. Первый способ: использовать Инспектор объектов, предварительно указав любой узел:

Выбрав нужную систему координат, нажмем Enter для подтверждения. Обратите внимание, что теперь координаты для любых узлов модели, в Инспекторе объектов будут показаны в выбранной системе:

Развернув список Координаты, мы получаем доступ к редактируемым полям:

Второй способ: открыть таблицу с данными об узлах. Это можно сделать например так: Вид - Таблицы - Узлы. В таблице вызовем из контекстного меню знакомый диалог Колонки таблицы:

Перейдем к нагрузкам, выбрав узловые нагрузки. Для ориентации приложенных усилий в пространстве, необходимо использовать поля Угол (если направление действия нагрузок отличаются от направления в глобальной системе координат)

Рассмотрим как будет меняться приложенная горизонтальная сила в зависимости от изменения угла в каждом из полей по очереди. Самый первый вариант, все углы равны 0:

Изменим значение в первом поле, картинка почти не изменилась, сила вращается относительно оси Х (угол Гамма):

Теперь повернем относительно оси Y (угол Бета):

И последний поворот относительно оси Z (угол Альфа):

Значения задаваемых углов могут быть как положительными, так и отрицательными.
Рассмотрим, как получить реакции для наклонной стойки. По умолчанию заделка представлена вот такими кубиками:

Чтобы увеличить информативность, зайдем в меню Показать и настроим отображение опор следующим образом:

Обратите внимание, цвета направлений в опоре совпадают со цветом осей глобальной системы координат. Откроем меню Результаты - Эпюры для стержней - Реакции:

Можно заметить, что включение/выключения флажка Реакции в местной системе, никак не влияет на реакции. Необходимо внести изменения в свойство опор. Для этого создадим новую метку и обратим внимание на выделенный фрагмент:

Щелкнем по кнопке Направления и попадем в диалог, который позволит нам сориентировать опору в нужном направлении:

В этом диалоге углы поворота относительно глобальных осей уже подписаны - Альфа, Бета и Гамма. Нам удобнее всего будет задать угол указав узел. Необязательно вручную вписывать номер узла, достаточно указать на него курсором (верхний узел наклонной стойки). После нажатия кнопки ОК, информация в поле Угол изменилась:

Применим данную опору к нижнему узлу наклонной стойки:

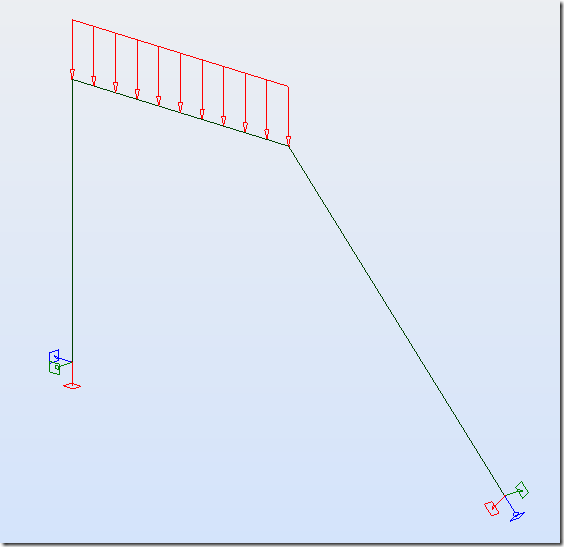
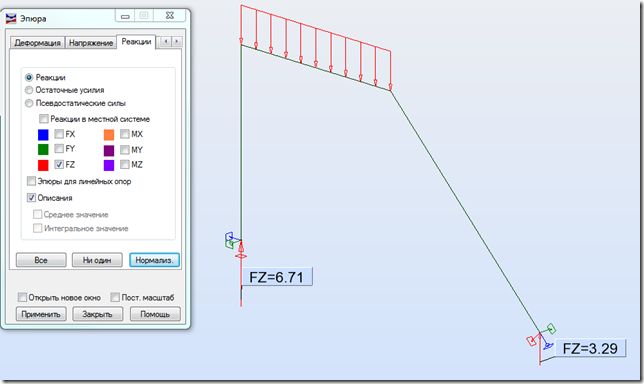
Ось Х опоры сориентирована вдоль стойки, так как мы и указали. Теперь проверим реакции:

Если нам все также интересны реакции в глобальной системе координат, достаточно снять флажок и выбрать нужный компонент:

В таблице реакций тоже предусмотрена возможность получить результаты в локальной системе. Для этого в контекстном меню Колонки таблицы необходимо выбрать указанный параметр:

Обратите внимание, что в заголовке окна указывается в какой системе представлены реакции.